SICP 习题全解 (1)

Exercise 1.1

 110
 210
 3
 4(+ 5 3 4)
 512
 6
 7(- 9 1)
 88
 9
10(/ 6 2)
113
12
13(+ (* 2 4) (- 4 6))
146
15
16(define a 3) 
17a
18
19(define b (+ a 1)) //b 4
20b
21
22(+ a b (* a b))
2319
24
25(= a b)
26#f
27
28(if (and (> b a) (< b (* a b)))
29		b 
30		a)
314
32
33(cond ((= a 4) 6)
34			((= b 4) (+ 6 7 a))
35			(else 25))
3616
37
38(+ 2 (if (> b a) b a))
396
40
41(* (cond ((> a b) a) 
42				 ((< a b) b)
43				 (else -1)) 
44   (+ a 1))
4516

Exercise 1.2

1(/ (+ 5 
2			4 
3			(- 2 
4      	 (- 3 
5         		(+ 6 
6            	 (/ 4 5)))))
7		(* 3 
8    	 (- 6 2) 
9       (- 2 7)))

Exercise 1.3

1(define (square x)
2    (* x x))
3
4(define (sum-of-the-two-larger-number x y z)
5    (cond ((and (> x z) (> y z)) (+ (square x) (square y)))
6        	((and (> x y) (> z y)) (+ (square x) (square z)))
7        	((and (> z x) (> y x)) (+ (square z) (square y)))))

Exercise 1.4

1(define (a-plus-abs-b a b) 
2  ((if (> b 0) + -) a b))

Model of evaluation allows for combinations whose operators are compound expressions.

这里 (if (> b 0) + -) 是一个复合表达式的组合式，它作为了运算符，也很好理解，从 procedure 的名字可以看出，过程的行为是 a+|b|，当 b>0 时，返回值是 a+b，而当 a<b 时，返回值为 a-b。

Exercise 1.5

1(define (p) (p)) 
2(define (test x y)
3	(if (= x 0) 0 y))
4
5(test 0 (p))

首先，可以确定的是，无论解释器使用的是什么求值方式，调用 (p) 总是进入一个无限循环 (infinite loop)，因为函数 p 会不断调用自身。

在应用序中，所有被传入的实际参数都会立即被求值，因此，在使用应用序的解释器里执行 (test 0 (p)) 时，实际参数 0 和 (p) 都会被求值，而对 (p) 的求值将使解释器进入无限循环，因此，如果一个解释器在运行 Ben 的测试时陷入停滞，那么这个解释器使用的是应用序求值模式。

另一方面，在正则序中，传入的实际参数只有在有需要时才会被求值，因此，在使用正则序的解释器里运行 (test 0 (p)) 时，0 和 (p) 都不会立即被求值，当解释进行到 if 语句时，形式参数 x 的实际参数 (也即是 0) 会被求值 (求值结果也是为 0)，然后和另一个 0 进行对比 ((= x 0))，因为对比的值为真 (#t)，所以 if 返回 0 作为值表达式的值，而这个值又作为 test 函数的值被返回。

因为在正则序求值中，调用 (p) 从始到终都没有被执行，所以也就不会产生无限循环，因此，如果一个解释器在运行 Ben 的测试时顺利返回 0，那么这个解释器使用的是正则序求值模式。

参考资料 https://sicp.readthedocs.io/en/latest/chp1/5.html

Exercise 1.6

sqrt-iter 函数，如果使用 trace 来跟踪它的调用过程的话，就会发现它执行了大量的递归调用，这些调用数量非常庞大，最终突破解释器的栈深度，造成错误。

if 语句是一种特殊形式，当它的 predicate 部分为真时，then-clause 分支会被求值，否则的话，else-clause 分支被求值，两个 clause 只有一个会被求值。

而另一方面，新定义的 new-if 只是一个普通函数，它没有 if 所具有的特殊形式，根据解释器所使用的应用序求值规则，每个函数的实际参数在传入的时候都会被求值，因此，当使用 new-if 函数时，无论 predicate 是真还是假，then-clause 和 else-clause 两个分支都会被求值。

参考资料 https://sicp.readthedocs.io/en/latest/chp1/6.html

Exercise 1.7

 1(define (good-enough? guess x)
 2    (< (abs (- (improve guess x) guess)) 0.001))
 3
 4我的答案还是取了差值，还是没有解决问题
 5
 6(define (good-enough? old-guess new-guess)
 7    (> 0.01
 8       (/ (abs (- new-guess old-guess))
 9          old-guess)))
10
11网上的答案取了变化率，当变化率小于1%时，就good enough了
12
13(define (sqrt-iter guess x)
14    (if (good-enough? guess (improve guess x))  ; 调用新的 good-enough?
15        (improve guess x)
16        (sqrt-iter (improve guess x)
17                   x)))
18但是他的解法需要修改原来的程序。
19
20(define (good-enough? guess x)
21    (< (/ (abs (- (improve guess x) guess)) guess) 0.01))
22修改我的代码，不用修改原来的程序。

Exercise 1.8

写一个修改版的 improve 过程即可。

1(define (improve guess x)
2    (/ (+ (/ x (square guess)) (* 2 guess)) 3))

Exercise 1.9

 1(define (+ a b)
 2(if (= a 0) b (inc (+ (dec a) b))))
 3;recursive process
 4(+ 4 5)
 5(inc (+ 3 5))
 6(inc (inc (+ 2 5)))
 7(inc (inc (inc (+ 1 5))))
 8(inc (inc (inc (inc(+ 0 5)))))
 9(inc (inc (inc (inc 5))))
10(inc (inc (inc 6)))
11(inc (inc 7))
12(inc 8)
139

从计算过程中可以很明显地看到伸展和收缩两个阶段，且伸展阶段所需的额外存储量和计算所需的步数都正比于参数 a，说明这是一个线性递归计算过程 (recursive process)。

1(define (+ a b)
2(if (= a 0) b (+ (dec a) (inc b))))
3;iterative process
4(+ 4 5)
5(+ 3 6)
6(+ 2 7)
7(+ 1 8)
8(+ 0 9)
99

从计算过程中可以看到，这个版本的 plus 函数只使用常量存储大小，且计算所需的步骤正比于参数 a，说明这是一个线性迭代计算过程 (iterative process)。

Exercise 1.10

1(define (A x y) 
2  (cond ((= y 0) 0)
3				((= x 0) (* 2 y))
4				((= y 1) 2)
5				(else (A (- x 1) (A x (- y 1))))))
6;Ackermann’s function.

手算我是不大行了，我改写成了 go 代码如下，运行结果：

 1func A(x, y int) int {
 2	if y == 0 {
 3		return 0
 4	}
 5	if x == 0 {
 6		return 2 * y
 7	}
 8	if y == 1 {
 9		return 2
10	}
11	return A(x-1, A(x, y-1))
12}
13//Ackermann’s function.
14//(A 1 10)   1024
15//(A 2 4)    65536
16//(A 3 3)    65536

数学表达式：

1(define (f n) (A 0 n))

推导易得： $$ f(n)=2*n $$

1(define (g n) (A 1 n))

推导易得： $$ g(n)=2^n $$

1(define (h n) (A 2 n))

函数 h 计算的是连续求 n 次二次幂，即 $$ 2^{2^{.^{。2}}} $$

Exercise 1.11

递归过程的代码很直接：

1(define (f *n*)
2	(if (< n 3) 
3      n
4      (+ (f (- n 1))
5				 (* 2 (f (- n 2)))
6				 (* 3 (f (- n 3)))))))
7;recursive process

迭代过程的代码可以参考书中求 fib 的过程完成：

1(define (f-iter a b c cnt)
2(if (= cnt 0) 
3    a
4    (f-iter b c (+ (* 3 a ) (* 2 b) c) (- cnt 1))
5))
6;iterative process

Exercise 1.12

用 Scheme 实在是不大会写：

 1(define (pascal row col)
 2    (cond ((> col row)
 3            (error "unvalid col value"))
 4          ((or (= col 0) (= row col))
 5            1)
 6          (else (+ (pascal (- row 1) (- col 1))
 7                   (pascal (- row 1) col)))))
 8;recursive process
 9
10;公式求杨辉三角数
11(define (pascal row col)
12    (/ (factorial row)
13       (* (factorial col)
14          (factorial (- row col)))))
15;iterative process

$$ pascal(col,row)=\frac {row!} {col!·(row-col)!} $$

https://sicp.readthedocs.io/en/latest/chp1/12.html

Exercise 1.13

数学证明没啥兴趣

Exercise 1.14

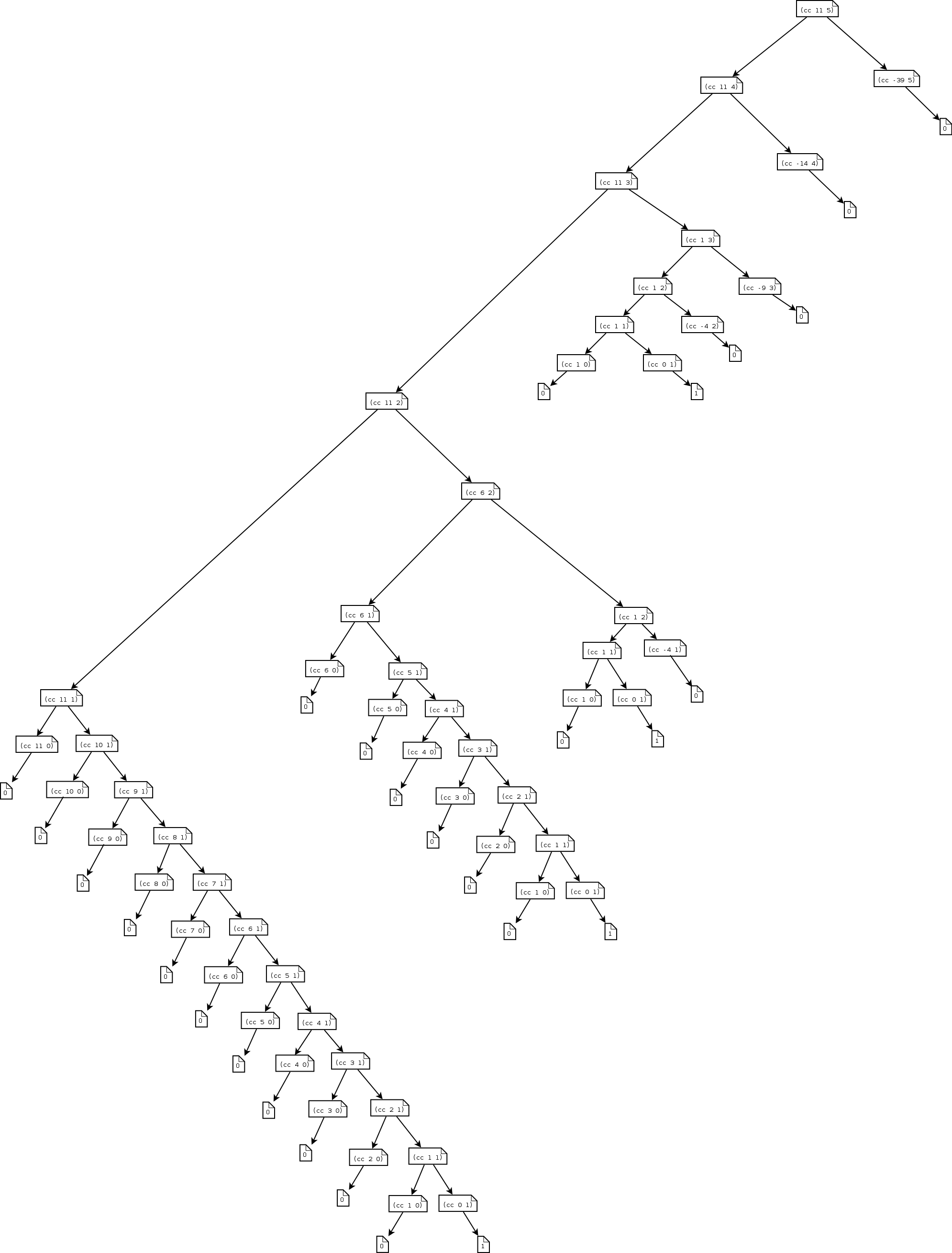
tree recursive

Exercise 1.15

https://sicp.readthedocs.io/en/latest/chp1/15.html

1(define (cube x) (* x x x))
2
3(define (p x) (- (* 3 x) (* 4 (cube x))))
4
5(define (sine angle)
6    (if (not (> (abs angle) 0.1))
7        angle
8        (p (sine (/ angle 3.0)))))

a) How many times is the procedure p applied when(sine 12.15) is evaluated？

p 共运行了 5 次

b)What is the order of growth in space and number of steps (as a function of a) used by the process generated by the sine procedure when (sine a) is evaluated？

在求值 (sine a) 的时候，a 每次都被除以 3.0，而 sine 是一个递归程序，因此它的时间和空间复杂度都是 O(log a)，每当 a 增大一倍 (准确地说，是乘以因子 3)，p 的运行次数就会增加一次。

Exercise 1.16

 1(define (fast-expt b n)
 2    (expt-iter b n 1))
 3
 4(define (expt-iter b n a)
 5    (cond ((= n 0)
 6            a)
 7          ((even? n)
 8            (expt-iter (square b)
 9                       (/ n 2)
10                       a))
11          ((odd? n)
12            (expt-iter b
13                       (- n 1)
14                       (* b a)))))

利用恒等式： $$ (b^\frac {n} {2})^2 = (b^2)^\frac {n} {2} $$ 不变量 a*b^n，当 n 从 n 变化到 0 时，a 就等于 b^n，当 n 为奇数时，a*b^n 和 a*b*b^n-1 相等，当 n 为偶数时，a*b^n 和 a*(b^2)^(n/2) 相等。翻译成 go 代码如下：

 1func fastExp(b, n int) int {
 2	var fastExpIter func(a, b, n int) int
 3	fastExpIter = func(a, b, n int) int {
 4		if n == 0 {
 5			return a
 6		}
 7		if n%2 == 0 {
 8			return fastExpIter(a, b*b, n/2)
 9		} else {
10			return fastExpIter(a*b, b, n-1)
11		}
12	}
13	return fastExpIter(1, b, n)
14}

Exercise 1.17

用 go 来描述：

 1func multi(a, b int) int {
 2	if b == 0 {
 3		return 0
 4	}
 5	if b%2 == 0 {
 6		return multi(a, b>>1) << 1
 7	} else {
 8		return a + multi(a, b-1)
 9	}
10}
11//recursive process

迭代形式参考 Exercise 1.18。

Exercise 1.18

 1func multi(a,b int) int{
 2	var multiIter func(a,b,res int) int
 3	multiIter = func(a, b, res int) int {
 4		if b==0{
 5			return res
 6		}
 7		if b%2==0 {
 8			return multiIter(a<<1,b>>1,res)
 9		}else {
10			return multiIter(a,b-1,res+a)
11		}
12	}
13	return multiIter(a,b,0)
14}
15//iterative process

Exercise 1.19

大概就是矩阵快速幂 (幸好这些内容我有基础) $$ \left (\begin {matrix} 1 & 1 \1 & 0 \\end {matrix}\right)* \left (\begin {matrix} f(n-1)\ f(n-2)\\end {matrix}\right) = \left (\begin {matrix} f(n)\ f(n-1)\\end {matrix}\right) $$ 即求左边这个矩阵的 n 次幂，可以用到之前的快速幂算法。

 1(define (fib n)
 2    (fib-iter 1 0 0 1 n))
 3
 4(define (fib-iter a b p q n)
 5    (cond ((= n 0)
 6            b)
 7          ((even? n)
 8            (fib-iter a 
 9                      b
10                      (+ (square p) (square q))     ; 计算 p'
11                      (+ (* 2 p q) (square q))      ; 计算 q'
12                      (/ n 2)))
13          (else
14            (fib-iter (+ (* b q) (* a q) (* a p))
15                      (+ (* b p) (* a q))
16                      p
17                      q
18                      (- n 1)))))

参考 https://sicp.readthedocs.io/en/latest/chp1/19.html 此题相当于特别实现了二阶矩阵的乘法。

通用的算法即是实现矩阵的乘法，利用快速幂即可解决此类问题。

Exercise 1.20

应用序和正则序 https://sicp.readthedocs.io/en/latest/chp1/20.html

Exercise 1.21

1(smallest-divisor 199)
2199
3(smallest-divisor 1999)
41999
5(smallest-divisor 19999)
67

Exercise 1.22

简单题，不做了。

https://sicp.readthedocs.io/en/latest/chp1/22.html

Exercise 1.23

简单题，不做了。

https://sicp.readthedocs.io/en/latest/chp1/23.html

Exercise 1.24

简单题，不做了。

https://sicp.readthedocs.io/en/latest/chp1/24.html

Exercise 1.25

数太大，没有办法求完幂再求余，因为费马检查在对一个非常大的数进行素数检测的时候，可能需要计算一个很大的乘幂，比如说，求十亿的一亿次方，这种非常大的数值计算的速度非常慢，而且很容易因为超出实现的限制而造成溢出。而书本的 expmod 函数，通过每次对乘幂进行 remainder 操作，从而将乘幂限制在一个很小的范围内 (不超过参数 m)，这样可以最大限度地避免溢出，而且计算速度快得多。

Exercise 1.26

1(expmod base (/ exp 2) m) ;算了两遍

所以每次当 exp 为偶数时，Louis 的 expmod 过程的计算量就会增加一倍，因此原本 Θ(log⁡n) 的计算过程变成了 Θ(n)。

Exercise 1.27

 1(define (carmichael-test n)
 2    (test-iter 1 n))
 3
 4(define (test-iter a n)
 5    (cond ((= a n)
 6            #t)
 7          ((congruent? a n)
 8            (test-iter (+ a 1) n))
 9          (else
10            #f)))
11
12(define (congruent? a n)           ; 同余检测
13    (= (expmod a n n) a))

将这个测试函数称之为 carmichael-test，对于给定参数 n，它要检验所有少于 n 的数 a，a^n 是否都与 a 模 n 同余。

Exercise 1.28

证明参考 wiki 米勒罗宾素数测试

这里的 nontrivial square root of 1 modulo n 意思是，如果 a^2mod n == 1,n 必定不是素数，在快速幂里面加上这一步验证即可，附上用 go 写的代码：

 1func millerRabinPrimeTest(n int) bool {
 2	var testIter func(times int) bool
 3	testIter = func(times int) bool {
 4		if times == 0 {
 5			return true
 6		}
 7		if fastExpMod(nonZeroRandom(n), n-1, n) == 1 {
 8			return testIter(times - 1)
 9		} else {
10			return false
11		}
12	}
13	return testIter(n / 2)
14}
15
16func nonZeroRandom(n int) int {
17	r := rand.Intn(n)
18	if r == 0{
19		return nonZeroRandom(n)
20	}else {
21		return r
22	}
23}
24
25func nontrivialSquareRoot(a, n int) bool {
26	return a != 1 && a != n-1 && (a*a)%n == 1
27}
28
29func square(x int) int {
30	return x * x
31}
32
33func fastExpMod(base, exp, mod int) int {
34	if exp == 0 {
35		return 1
36	}
37	if nontrivialSquareRoot(base, mod) {
38		return 0
39	}
40	if exp%2 == 0 {
41		return square(fastExpMod(base, exp/2, mod)) % mod
42	} else {
43		return (base * fastExpMod(base, exp-1, mod)) % mod
44	}
45}

Exercise 1.29

 1def sum(term, a, next, b):
 2    if a > b:
 3        return 0
 4    return term(a) + sum(term, next(a), next, b)
 5
 6
 7def simpson(f, a, b, n):
 8    h = (b - a) / n
 9
10    def y(k):
11        return f(a + k * h)
12
13    def factor(k):
14        if k == 0 or k == n:
15            return 1
16        if k % 2 == 1:
17            return 4
18        if k % 2 == 0:
19            return 2
20
21    def term(k):
22        return factor(k) * y(k)
23
24    def next(k):
25        return k + 1
26
27    if n % 2 != 0:
28        print("error n can not be odd")
29    return (h / 3) * sum(term, 0, next, n)
30
31
32def cube(x):
33    return x * x * x
34
35
36if __name__ == '__main__':
37    import sys
38    sys.setrecursionlimit(3000)
39    print(simpson(cube, 0, 1, 100))
40    print(simpson(cube, 0, 1, 1000))

Exercise 1.30

1def sum(term, a, next, b):
2    def iter(a, result):
3        if a > b:
4            return result
5        else:
6            return iter(next(a), term(a) + result)
7
8    return iter(a, 0)

Exercise 1.31

 1def product(factor, a, next, b):
 2    if a > b:
 3        return 1
 4    else:
 5        return factor(a) * product(factor, next(a), next, b)
 6
 7
 8def pi(n):
 9    def factor(n):
10        if n % 2 == 1:
11            molecular = n + 1  # 分子
12            denominator = n + 2  # 分母
13        else:
14            molecular = n + 2  # 分子
15            denominator = n + 1  # 分母
16        return molecular / denominator
17
18    def next(n):
19        return n + 1
20
21    return 4 * product(factor, 1, next, 1000)
22
23
24if __name__ == '__main__':
25    import sys
26    sys.setrecursionlimit(3000)
27    
28    print(pi(1000))

1def product(factor, a, next, b):
2    def iter(a, result):
3        if a > b:
4            return result
5        else:
6            return iter(next(a), result * factor(a))
7
8    return iter(a, 1)

Exercise 1.32

1def accumulate(combiner, null_value, term, a, next, b):
2    if a > b:
3        return null_value
4    else:
5        return combiner(term(a), accumulate(combiner, null_value, term, next(a), next, b))

1def accumulate(combiner, null_value, term, a, next, b):
2    def iter(a, result):
3        if a > b:
4            return result
5        else:
6            return iter(next(a), combiner(term(a), result))
7
8    return iter(a, null_value)

Exercise 1.33

 1import random
 2
 3
 4def filter_accumulate(combiner, null_value, term, a, next, b, filter):
 5    if a > b:
 6        return null_value
 7    else:
 8        if filter(a):
 9            return combiner(term(a), filter_accumulate(combiner, null_value, term, next(a), next, b, filter))
10        else:
11            return filter_accumulate(combiner, null_value, term, next(a), next, b, filter)
12
13
14def square(x):
15    return x * x
16
17
18def is_nontrivial_square_root(a, mod):
19    return a != 1 and a != mod - 1 and a * a % mod == 1
20
21
22def fast_exp(a, b, mod):
23    if b == 0:
24        return 1
25    if is_nontrivial_square_root(a, mod):
26        return 0
27    if b % 2 == 0:
28        return square(fast_exp(a, b / 2, mod)) % mod
29    else:
30        return a * fast_exp(a, b - 1, mod) % mod
31
32
33def rand(n):
34    return random.randint(1, n - 1)
35
36
37def is_prime(n):
38    if n == 1:
39        return False
40
41    def iter(times):
42        if times == 0:
43            return True
44        if fast_exp(rand(n), n - 1, n) == 1:
45            return iter(times - 1)
46        else:
47            return False
48
49    return iter(n//2)
50
51
52def plus(x, y):
53    return x + y
54
55
56def identity(x):
57    return x
58
59
60def next(x):
61    return x + 1
62
63
64def sum_of_prime(a, b):
65    return filter_accumulate(plus, 0, identity, a, next, b, is_prime)
66
67
68def gcd(a, b):
69    if b == 0:
70        return a
71    else:
72        return gcd(b, a % b)
73
74
75def multi(x, y):
76    return x * y
77
78
79def sum_of_relatively_prime(n):
80    def is_relatively_prime(a):
81        return gcd(a, n) == 1
82
83    return filter_accumulate(multi, 1, identity, 1, next, n, is_relatively_prime)
84
85
86if __name__ == '__main__':
87    print(sum_of_prime(1,10)) # 17
88    print(sum_of_relatively_prime(10)) # 189

Exercise 1.35

 1tolerance = 0.0001
 2
 3
 4def fixed_point(f, first_guess):
 5    def close_enough(v1, v2):
 6        return abs(v1 - v2) < tolerance
 7
 8    def helper(guess):
 9        next_guess = f(guess)
10        if close_enough(guess, next_guess):
11            return next_guess
12        return helper(next_guess)
13
14    return helper(first_guess)
15
16
17def golden_ratio():
18    return fixed_point(lambda x: 1 + 1 / x, 1) # 1.6180555555555556

Exercise 1.36

 1def fixed_point_modified(f, first_guess):
 2    def close_enough(v1, v2):
 3        return abs(v1 - v2) < tolerance
 4
 5    def helper(guess):
 6        next_guess = f(guess)
 7        print(next_guess)
 8        if close_enough(guess, next_guess):
 9            return next_guess
10        return helper(next_guess)
11
12    return helper(first_guess)
13
14
15def average_damping(f):
16    return lambda x: (x + f(x)) / 2
17
18
19if __name__ == '__main__':
20    print(fixed_point_modified(lambda x: log(1000) / log(x), 10))
21    print("---------------------")
22    print(fixed_point_modified(average_damping(lambda x: log(1000) / log(x)), 10))
23    
24# 2.9999999999999996
25# 6.2877098228681545
26# 3.7570797902002955
27# 5.218748919675316
28# 4.1807977460633134
29# 4.828902657081293
30# 4.386936895811029
31# 4.671722808746095
32# 4.481109436117821
33# 4.605567315585735
34# 4.522955348093164
35# 4.577201597629606
36# 4.541325786357399
37# 4.564940905198754
38# 4.549347961475409
39# 4.5596228442307565
40# 4.552843114094703
41# 4.55731263660315
42# 4.554364381825887
43# 4.556308401465587
44# 4.555026226620339
45# 4.55587174038325
46# 4.555314115211184
47# 4.555681847896976
48# 4.555439330395129
49# 4.555599264136406
50# 4.555493789937456
51# 4.555563347820309
52# 4.555563347820309
53# ---------------------
54# 6.5
55# 5.095215099176933
56# 4.668760681281611
57# 4.57585730576714
58# 4.559030116711325
59# 4.55613168520593
60# 4.555637206157649
61# 4.55555298754564
62# 4.55555298754564

可以看到，用了 average_damping 的过程收敛速度明显变快。

Exercise 1.37

 1def cont_frac(n, d, k):
 2    def helper(i):
 3        if i == k:
 4            return n(i) / d(i)
 5        else:
 6            return n(i) / (d(i) + helper(i + 1))
 7
 8    return helper(1)
 9  
10if __name__ == '__main__':
11    print(
12        cont_frac(
13            lambda i: 1,
14            lambda i: 1,
15            100
16        )
17    )
18# 0.6180339887498948

1def cont_frac_iter(n, d, k):
2    def helper(i, res):
3        if i == 0:
4            return res
5        else:
6            return helper(i - 1, n(i) / (d(i) + res))
7
8    return helper(k, 0)

Exercise 1.38

 1def approximate_e(k):
 2    def d(i):
 3        if (i + 1) % 3 == 0:
 4            return (i + 1) / 3 * 2
 5        else:
 6            return 1
 7
 8    return 2 + cont_frac_iter(lambda i: 1, d, k)
 9
10
11if __name__ == '__main__':
12    print(approximate_e(100))
13# 2.7182818284590455

Exercise 1.39

 1def tan_cf(x, k):
 2    def n(i):
 3        if i == 1:
 4            return x
 5        else:
 6            return - x * x
 7
 8    return cont_frac(n, lambda i: 2 * i - 1, k)
 9
10
11if __name__ == '__main__':
12    print(tan_cf(0,100))
13    print(tan_cf(3.1415926/2,100))
14# 0.0
15# 37320539.58514773 相当于无穷大，因为这里的 pi，是近似值

Exercise 1.40

1def cubic(a, b, c):
2    return newtons_method(lambda x: cube(x) + a * square(x) + b * x + c, 1.0)

Exercise 1.41

1def inc(x):
2    return x + 1
3
4
5def double(f):
6    return lambda x: f(f(x))
7  
8double(double(double))(inc)(5) 
9# 21

Exercise 1.42

1def compose(f, g):
2    return lambda x: f(g(x))

Exercise 1.43

 1def repeated(f, n):
 2    if n == 1:
 3        return f
 4    else:
 5        return compose(f, repeated(f, n - 1))
 6# recursive
 7def repeated_iter(f, n):
 8    def _iter(times, repeated_f):
 9        if times == 1:
10            return repeated_f
11        else:
12            return _iter(times - 1, compose(f, repeated_f))
13
14    return _iter(n, f)
15# iterative

Exercise 1.44

1def smooth(f):
2    dx = 0.00001
3    return lambda x: (f(x - dx) + f(x) + f(x + dx)) / 3
4
5
6def n_fold_smoothed(f, n):
7    return repeated(smooth, n)(f)

Exercise 1.45

 1def nth_root(n):
 2    def root(x):
 3        k = math.floor(math.log2(n))
 4
 5        def f(y):
 6            return x / exp(y, n - 1)
 7
 8        return fix_point_of_transform(f, repeated(average_damping, k), 1.0)
 9
10    return root

Exercise 1.46

 1def iterative_improve(good_enough, improve_method):
 2    def helper(guess):
 3        next_guess = improve_method(guess)
 4        if good_enough(guess, next_guess):
 5            return next_guess
 6        else:
 7            return helper(next_guess)
 8
 9    return helper
10
11
12def sqrt_by_iterative_improve(x):
13    def close_enough(v1, v2):
14        return abs(v1 - v2) < tolerance
15
16    def f(y):
17        return x / y
18
19    return iterative_improve(close_enough, average_damping(f))(1.0)
20
21
22def fixed_point(f, first_guess):
23    def close_enough(v1, v2):
24        return abs(v1 - v2) < tolerance
25
26    return iterative_improve(close_enough, f)(first_guess)

Zwlin's Blog

SICP 习题全解 (1)

Last updated: 2021/07/31 Published at: 2021/07/31

Exercise 1.1

Exercise 1.2

Exercise 1.3

Exercise 1.4

Exercise 1.5

Exercise 1.6

Exercise 1.7

Exercise 1.8

Exercise 1.9

Exercise 1.10

Exercise 1.11

Exercise 1.12

Exercise 1.13

Exercise 1.14

Exercise 1.15

Exercise 1.16

Exercise 1.17

Exercise 1.18

Exercise 1.19

Exercise 1.20

Exercise 1.21

Exercise 1.22

Exercise 1.23

Exercise 1.24

Exercise 1.25

Exercise 1.26

Exercise 1.27

Exercise 1.28

Exercise 1.29

Exercise 1.30

Exercise 1.31

Exercise 1.32

Exercise 1.33

Exercise 1.35

Exercise 1.36

Exercise 1.37

Exercise 1.38

Exercise 1.39

Exercise 1.40

Exercise 1.41

Exercise 1.42

Exercise 1.43

Exercise 1.44

Exercise 1.45

Exercise 1.46